Introduction
MIDI Keyboards are tuned in a system in which all half steps have the same distance from the next one (twelfth root of two). This is what we call a 12-tone equal-tempered scale[1]. This system is actually very young; it was introduced in the 19th century and has its main right in systems like the system of Schoenberg with 12 tones "just related to each other"[2]. If we go back in history to works like the "Fitzwilliam Virginal Book" or even Bach's "Wohltemperiertes Clavier", or if we go to non-western music like Arabic scales or the Gamelan, or finally if we are working with so-called microtonal scales (third-tone, quarter-tone or whatever), we need a keyboard which can easily be tuned to any scale we wish. I want to show how such a keyboard can be built in Csound. I will use Andrés Cabrera's QuteCsound as a frontend because of its simple and intuitive Graphical User Interface. Of course it is possible to implement the code in other environments too, such as TCL/TK.[3].
I. General MIDI Configuration (tune_01.csd)
Before we come to our proper subject, we must configure our orchestra for receiving MIDI. There is a very simple way to get your keyboard signals (which key you press or release and the related velocity) into Csound. You just have to adjust your Csound Options to read something like this:[4]
-odac -Ma -b128 -B512 --midi-key=4 --midi-velocity-amp=5
The meaning of these flags are:
- -odac : assigns the audio output to the dac[5]
- -Ma : assigns all MIDI input devices to Csound[6]
- -b128 -B512 : sets the software (-b) and the hardware (-B) buffer size [7]
- --midi-key=4 --midi-velocity-amp=5 : These flags set the incoming MIDI data to the p-fields of a Csound instrument. --midi-key=4 lets our instrument receive the MIDI key number as p4. --midi-velocity-amp=5 sends the velocity of a pressed key as an amplitude value on p5.
With these flags, all incoming MIDI data from MIDI channel 1 are assigned to instrument 1, from channel 2 to instrument 2, and so on. If we want to pass the MIDI events from all channels to instrument 1, we must use the statement massign 0,1. So let us check our MIDI configuration using this simple instrument:
<CsoundSynthesizer> <CsOptions> -odac -Ma -b128 -B512 --midi-key=4 --midi-velocity-amp=5 </CsOptions> <CsInstruments> massign 0, 1 instr 1 anote oscils p5, cpsmidinn(p4), 0 kenv linsegr 0, .1, 1, p3-0.1, 1, .1, 0 out anote * kenv endin </CsInstruments> <CsScore> f 0 3600 e </CsScore> </CsoundSynthesizer>All the CSD example files for this article are available here. TuningExs.zip.
II. Playing with Cent Deviations (tune_02.csd)
If we divide an octave into 1200 equal parts, we call one of these parts a cent. It is a common and reasonable unit for expressing differences in tuning. We can say that the acoustically pure fifth (with the ratio 3:2) is 2 cents smaller than the equal-tempered fifth[8], or the acoustically pure major third is nearly 14 cents lower than the equal-tempered one. So we can make a list of the cent deviations we wish to have in comparison with the standard equal-tempered tuning. For example, the following is a list from the first half-step to the twelfth. It belongs to the so called middle tone tuning after Zarlino ("Dimostratione harmoniche", 1571):[9]
0 -34 -7 10 -14 3 -21 -3 -27 -10 7 -17We get this list into Csound by creating a function table: [10]
giScale ftgen 1, 0, -12, -2, 0, -34, -7, 10, -14, 3, -21, -3, -27, -10, 7, -17
What we need now is a way to access the appropriate cent value in the table when we press a key. We can do so using the Modulus operator. Each "C" note (i.e. the MIDI note numbers 24, 36, 48, ...) returns 0 as modulo 12; each "C#" returns 1 as modulo 12, and so on. So we can use these values as indices for our function tables. Then we build a fractional value from the stripped cent deviation by using the cent opcode. So this is the next instrument:
<CsoundSynthesizer> <CsOptions> -odac -Ma -b128 -B512 --midi-key=4 --midi-velocity-amp=5 -m0 </CsOptions> <CsInstruments> giScale ftgen 1, 0, -12, -2, 0, -34, -7, 10, -14, 3, -21, -3, -27, -10, 7, -17 massign 0, 1 instr 1 ikey = p4 ivel = p5 indx = ikey % 12 icent tab_i indx, 1 ifreqeq = cpsmidinn(ikey) ifreq = ifreqeq * cent(icent) prints "Key %d: equal-tempered frequency = %f;", ikey, ifreqeq prints "frequency with cent deviation %d = %f%n", icent,ifreq anote oscils ivel, ifreq, 0 kenv linsegr 0, .1, 1, p3-0.1, 1, .1, 0 out anote * kenv endin </CsInstruments> <CsScore> f 0 3600 e </CsScore> </CsoundSynthesizer>
As you see, it was decided to reduce the Csound printout by using the flag -m0. On the other hand the more verbose printout is possible using the Csound command line flag -v and any of the -m flags accompanied by the appropriate message level number.
III. Changing the Reference Tone and its Frequency (tune_03.csd)
At the moment the first position in our cent deviation list is always the note "C". If we want to transpose to a certain scale, say to "A" as reference tone instead of "C", we need a little calculation which allows the first position in the cent list be connected to each "A" which is pressed on the keyboard. This is done by employing the following code:
kfixtone invalue "fixtone" ishift = 12 - (i(kfixtone) % 12) indx = (ikey+ishift) % 12
In the first line, we simply receive the values from the widget panel of QuteCsound. In this case, a SpinBox is used, as show in Figure 1.
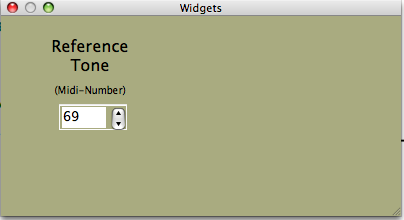
The channel of the SpinBox is called "reftone" and its value is assigned to the k-value kreftone. This is a k-value because it can be changed during the performance. But when we press a certain key, a new instance of instrument 1 is created, and in this context the key value and the connected table lookup operations become initialized, so we need to take the i-value of kreftone at the moment a new instance of instr 1 is called. This is done by the statement i(kreftone).
In the second line, the shift value is calculated. Here, we will get a shift value of 3 for an "A" pitch in any octave. If we add this shift value to the usual key value (e.g. 69), we get 0 as an index. That is what we wanted. Now the "A" has the cent deviation at index 0, the "B flat" at index 1, and so on. Below is the CSD for relating a scale to different reference tones:[11]
<CsoundSynthesizer> <CsOptions> -odac -Ma -b128 -B512 --midi-key=4 --midi-velocity-amp=5 -m0 </CsOptions> <CsInstruments> giScale ftgen 1, 0, -12, -2, 0, -34, -7, 10, -14, 3, -21, \ -3, -27, -10, 7, -17 massign 0, 1 instr 1 ikey = p4 ivel = p5 kreftone invalue "reftone"; any midi note number ishift = 12 - (i(kreftone) % 12); amount of shift for ... indx = (ikey+ishift) % 12; ... correct reading icent tab_i indx, 1 ifreqeq = cpsmidinn(ikey) ifreq = ifreqeq * cent(icent) prints "Key %d: equal-tempered frequency = %f;", ikey, ifreqeq prints "frequency with cent deviation %d = %f%n", icent,ifreq anote oscils ivel, ifreq, 0 kenv linsegr 0, .1, 1, p3-0.1, 1, .1, 0 out anote * kenv endin </CsInstruments> <CsScore> f 0 3600 e </CsScore> </CsoundSynthesizer>
IV. Changing the Reference Frequency (tune_04.csd)
Now we want to add a feature so that we can tell our instrument to accept any frequency for the reference key. The usual reference key is "A" (MIDI-Key 69) with a frequency of 440 Hertz, but in orchestral music the "A" is mostly employed at 443 Hz. In Ancient Music there is one "high" (465 Hz) and one "low" (415 Hz) tuning for the "A". And in contemporary music we want to be able to tune our instrument to any reference frequency, depending on the situation.
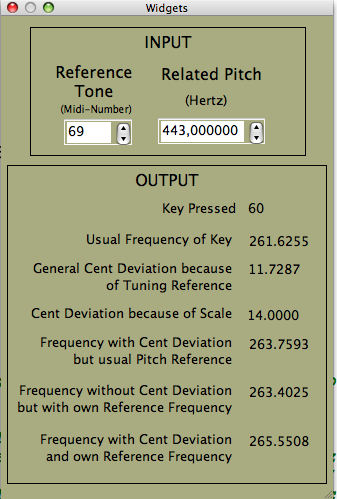
A simple way to include this feature in our code is to compare the standard frequency of a key (for instance 440 Hz) to the frequency we want to have (for instance 443 Hz), to calculate the difference in cents (in this case 11.7287 cents), and then to add this difference to the cent deviations we get by reading our function table. This is not the most elegant way to do this approach,[12] and there are some roundoff errors, but it is a simple method, and seems to give acceptable results. In our GUI we now add some more or less interesting information.
<CsoundSynthesizer>
<CsOptions>
-odac -Ma -b128 -B512 --midi-key=4 --midi-velocity-amp=5 -m0
</CsOptions>
<CsInstruments>
giScale ftgen 1, 0, -12, -2, 0, -34, -7, 10, -14, \
3, -21, -3, -27, -10, 7, -17
massign 0, 1
instr 1
;;INPUT
ikey = p4
ivel = p5
kreftone invalue "reftone"; any midi note number
ktunfreq invalue "tunfreq"; any frequency for it
ireftone = i(kreftone)
itunfreq = i(ktunfreq)
;;CALCULATION
;centdifference tuning freq to usual freq
icentdiff = 1200 * logbtwo(itunfreq / cpsmidinn(ireftone))
ishift = 12 - (ireftone % 12)
indx = (ikey+ishift) % 12
icent tab_i indx, 1; cent deviation according to function table
; frequency for equal tempered and usual referencecentdifference
; tuning freq to usual freq(a = 440 Hz)
ifreqeq = cpsmidinn(ikey)
; frequency for equal tempered on actual reference (tuning frequency)
ifreqeqtun = ifreqeq * cent(icentdiff)
; frequency regarding cent deviations but usual reference (a = 440 Hz)
ifreqscnorm = ifreqeq * cent(icent)
; frequency with correct cent deviations in scale and tuning pitch
ifreqsctun = ifreqeq * cent(icent + icentdiff)
anote oscils ivel, ifreqsctun, 0
kenv linsegr 0, .1, 1, p3-0.1, 1, .1, 0
out anote * kenv
;;SHOW OUTPUT
Skey sprintf "%d", ikey
outvalue "key", Skey
outvalue "centdiff", icentdiff
outvalue "cent", icent
outvalue "freqeq", ifreqeq
outvalue "freqscnorm", ifreqscnorm
outvalue "freqeqtun", ifreqeqtun
outvalue "freqsctun", ifreqsctun
endin
</CsInstruments>
<CsScore>
f 0 3600
e
</CsScore>
</CsoundSynthesizer>
V. Changing the Scales during Live-Performance (tune_05.csd, tune_05a.csd, tune_05b.csd)
If we have more than one scale and if we want to change the scales at any point in our performance, we can add this feature very easily to our instrument. We just add some function tables to the existing one. Then we put a menu widget in our QuteCsound GUI and transmit its value again via the invalue opcode. As the menu sends the integers 0, 1, 2, ... for the selected items, we just have to add 1 and take the result as the table number for tab_i. That is all we need to do.
<CsoundSynthesizer>
<CsOptions>
-odac -Ma -b128 -B512 --midi-key=4 --midi-velocity-amp=5 -m0
</CsOptions>
<CsInstruments>
;equal-tempered scale
giScale1 ftgen 1, 0, -12, -2, 0
;middle tone scale
giScale2 ftgen 2, 0, -12, -2, 0, -34, -7, 10, \
-14, 3, -21, -3, -27, -10, 7, -17
;pythagorean scale[13]
giScale3 ftgen 3, 0, -12, -2, 0, 14, 4, -6, 8, -2, 12, 2, 16, 6, -4, 10
massign 0, 1
instr 1
;;INPUT
ikey = p4
ivel = p5
kreftone invalue "reftone"; any midi note number
ktunfreq invalue "tunfreq"; any frequency for it
kscale invalue "scale"; select scale by menu
ireftone = i(kreftone)
itunfreq = i(ktunfreq)
iscale = i(kscale) + 1; menu item 0 selects function table 1 etc
;;CALCULATION
; centdifference tuning freq to usual freq
icentdiff = 1200 * logbtwo(itunfreq / cpsmidinn(ireftone))
shift = 12 - (ireftone % 12)
indx = (ikey+ishift) % 12
; cent deviation according to function table
icent tab_i indx, iscale
; frequency for equal tempered and usual reference (a = 440 Hz)
ifreqeq = cpsmidinn(ikey)
; frequency for equal tempered on actual reference (tuning frequency)
ifreqeqtun = ifreqeq * cent(icentdiff)
; frequency regarding cent deviations but usual reference (a = 440 Hz)
ifreqscnorm = ifreqeq * cent(icent)
; frequency with correct cent deviations in scale and tuning pitch
ifreqsctun = ifreqeq * cent(icent + icentdiff)
anote oscils ivel, ifreqsctun, 0
kenv linsegr 0, .1, 1, p3-0.1, 1, .1, 0
out anote * kenv
;;SHOW OUTPUT
Skey sprintf "%d", ikey
outvalue "key", Skey
outvalue "centdiff", icentdiff
outvalue "cent", icent
outvalue "freqeq", ifreqeq
outvalue "freqscnorm", ifreqscnorm
outvalue "freqeqtun", ifreqeqtun
outvalue "freqsctun", ifreqsctun
endin
</CsInstruments>
<CsScore>
f 0 3600
e
</CsScore>
</CsoundSynthesizer>
You may prefer to change the scale while playing on your MIDI keyboard using the number keys on your computer keyboard (1-9), or by some reserved keys on your MIDI keyboard. The CSD files tune_05a.csd and tune_05b.csd give examples for these cases.
VI. Playing Different Scales Simultaneously with Different Keyboards (tune_06.csd)
What if we like to play with more than one keyboard, each in a different scale? We can do this by sending keyboard 1 on MIDI-Channel 1, keyboard 2 on channel 2, and so on. The simplest way to split the incoming data is probably employing the following method: Copy the code of instr 1 and call it instr 2, then change the massign statement to that number, as indicated below.
massign 1, 1 massign 2, 2
We could also remove these statements altogether, because this is what Csound does by default: to send MIDI channel 1 to instrument 1, MIDI channel 2 to instrument 2, and so on.
Perhaps an even better way to do the same is to change the design of our instrument. As usual, we receive all incoming MIDI data in one instrument. Inside this instrument, we ask for the channel via the opcode midichn. Then we get the scale by the result of this opcode, and we can add a warning in the case that a channel is received which is not defined in the GUI.
<CsoundSynthesizer>
<CsOptions>
-odac -Ma -b128 -B512 --midi-key=4 --midi-velocity-amp=5 -m0
</CsOptions>
<CsInstruments>
;equal-tempered scale
giScale1 ftgen 1, 0, -12, -2, 0
;middle tone scale
giScale2 ftgen 2, 0, -12, -2, 0, -34, -7, 10, \
-14, 3, -21, -3, -27, -10, 7, - 17
;pythagorean scale
giScale3 ftgen 3, 0, -12, -2, 0, 14, 4, -6, 8, -2, 12, 2, 16, 6, -4, 10
massign 0, 1
instr 1
ikey = p4
ivel = p5
;;SELECT SCALE BY CHANNEL
kchan1 invalue "chan1"
kchan2 invalue "chan2"
kchan3 invalue "chan3"
kscale1 invalue "scale1"
kscale2 invalue "scale2"
kscale3 invalue "scale3"
ichn midichn
if ichn == i(kchan1) then
iscale = i(kscale1)
elseif ichn == i(kchan2) then
iscale = i(kscale2)
elseif ichn == i(kchan3) then
iscale = i(kscale3)
else
iscale = -1
endif
kreftone invalue "reftone"; any midi note number
ktunfreq invalue "tunfreq"; any frequency for it
kscale invalue "scale"; select scale by menu
ireftone = i(kreftone)
itunfreq = i(ktunfreq)
;;CALCULATION
; centdifference tuning freq to usual freq
icentdiff = 1200 * logbtwo(itunfreq / cpsmidinn(ireftone))
ishift = 12 - (ireftone % 12)
indx = (ikey+ishift) % 12
; cent deviation according to function table
icent tab_i indx, iscale
; frequency for equal tempered and usual reference (a = 440 Hz)
ifreqeq = cpsmidinn(ikey)
; frequency for equal tempered on actual reference (tuning frequency)
ifreqeqtun = ifreqeq * cent(icentdiff)
; frequency regarding cent deviations but usual reference (a = 440 Hz)
ifreqscnorm = ifreqeq * cent(icent)
; frequency with correct cent deviations in scale and tuning pitch
ifreqsctun = ifreqeq * cent(icent + icentdiff)
anote oscils ivel, ifreqsctun, 0
kenv linsegr 0, .1, 1, p3-0.1, 1, .1, 0
out anote * kenv
;;SHOW OUTPUT
Skey sprintf "%d", ikey
outvalue "key", Skey
if iscale == -1 then
outvalue "scale", "None!"
else
Schan sprintf "%d", iscale
outvalue "scale", Schan
endif
outvalue "centdiff", icentdiff
outvalue "cent", icent
outvalue "freqeq", ifreqeq
outvalue "freqscnorm", ifreqscnorm
outvalue "freqeqtun", ifreqeqtun
outvalue "freqsctun", ifreqsctun
endin
</CsInstruments>
<CsScore>
f 0 3600
e
VII. Having More (or Less) than 12 Tones per Octave (tune_07.csd)
Until now we have only dealt with 12 steps per octave. But we want to be able to play a third-tone scale (18 steps per octave), a quarter-tone scale (24 steps per octave) or whatever we like as an equal or not equal partition of the octave. We can express all of these partitions easily in cents, too; not in cent deviations from the equal-tempered scale, but in absolute cents, starting from the first step to the last step before reaching the octave. Here are some examples:
Equal-tempered Twelve tones (12 steps): 0 100 200 300 400 500 600 700 800 900 1000 1100 Third tones (18): 0 66.67 133.33 200 266.67 333.33 400 466.67 533.33 600 666.67 733.33 800 866.67 933.33 1000 1066.67 1133.33 Quarter tones (24): 0 50 100 150 200 250 300 350 400 450 500 550 600 650 700 750 800 850 900 950 1000 1050 1100 1150 Indian sruti (22):[14] 0 90 112 182 204 294 316 386 408 498 520 490 610 702 792 814 884 906 996 1018 1088 1110
Our goal in programming must be now to set the first step (cent = 0) to our reference key, and then to continue the cent steps to the "right" (1200 cents and higher) and to the "left" (lower than 0 cents). For instance, if our reference is MIDI key 69 with 440 Hz and we have a third-tone scale, our program shall look at key 68 for the same value as the last defined step (1133.33 cents), but an octave lower (1133.33 - 1200 = -66.67 cents). This is done using the following code:[15]
irelkey = 69 ipch = 440 itablen = 18 ; octave position ioct = floor((p4 - irelkey) / itablen) ; correct values > 0 but "mirror" values for < 0 indx1 = (p4-irelkey) % itablen ; so instead of -1 we get 17 now indx = (indx1 < 0 ? itablen + indx1 : indx1) ; so get the correct value from the centlist ... icent1 tab_i indx, iscale ; and modify it by the octave position icent = icent1 + (ioct * 1200) ; get the frequency at the end ifreq = ipch * cent(icent)
This is actually all we need. Now we can define whatever we want as a scale, with as many steps per octave we like, any relations between the steps we like, and our program will calculate the values and play it. Here is the code:
<CsoundSynthesizer>
<CsOptions>
-odac -Ma -b128 -B512 --midi-key=4 --midi-velocity-amp=5 -m0
</CsOptions>
<CsInstruments>
;;SCALES TO BE PLAYED
;Scale 1: Equal-tempered Twelve tones (12 steps per octave)
giHalfTones ftgen 1, 0, -12, -2, 0, 100, 200, 300, \
400, 500, 600, 700, 800, 900, 1000, 1100
;Scale 2: third-tones (18 steps per octave)
giThirTones ftgen 2, 0, -18, -2, 0, 66.67, 133.33, 200, 266.67, 333.33, \
400, 466.67, 533.33, 600, 666.67, 733.33, 800, 866.67, \
933.33, 1000, 1066.67, 1133.33
;Scale 3: Quarter Tones (24 steps per octave)
giQuarTones ftgen 3, 0, -24, -2, 0, 50, 100, 150, 200, 250, 300, 350,\
400, 450, 500, 550, 600, 650, 700, 750, 800, 850, 900, \
950, 1000, 1050, 1100, 1150
;Scale 4: Indian Sruti (22 steps per octave)
giSruti ftgen 4, 0, -22, -2, 0, 90, 112, 182, 204, 294, 316, 386, 408, \
498, 520, 490, 610, 702, 792, 814, 884, 906, 996, 1018, 1088, 1110
massign 0, 1
instr 1
;;INPUT
ikey = p4
ivel = p5
kreftone invalue "reftone"; any midi note number
ktunfreq invalue "tunfreq"; any frequency for it
kscale invalue "scale"; select scale by menu
ireftone = i(kreftone)
itunfreq = i(ktunfreq)
iscale = i(kscale) + 1; menu item 0 selects function table 1 etc
;;CALCULATION
itablen = ftlen(iscale)
;octave position
ioct = floor((p4 - ireftone) / itablen)
;correct values > 0 but negative for < 0
indx1 = (p4-ireftone) % itablen
; so instead of -1 we get 17 now
indx = (indx1 < 0 ? itablen + indx1 : indx1)
; get the correct value from the centlist ...
icent1 tab_i indx, iscale
; and modify it by the octave position
icent = icent1 + (ioct * 1200)
; get the frequency
ifreq = itunfreq * cent(icent)
anote oscils ivel, ifreq, 0
kenv linsegr 0, .1, 1, p3-0.1, 1, .1, 0
out anote * kenv
;;SHOW OUTPUT
Skey sprintf "%d", ikey
outvalue "key", Skey; key pressed
Scale sprintf "%d", iscale
outvalue "table", Scale; ftable number of scale
Steps sprintf "%d", itablen
outvalue "steps", Steps; number of steps in the scale
Sindx sprintf "%d", indx
outvalue "indx", Sindx; which step is selected by this key
outvalue "cent", icent; cent difference in relation to the reference frequency
outvalue "freq", ifreq
endin
</CsInstruments>
<CsScore>
f 0 9999
e
</CsScore>
</CsoundSynthesizer>
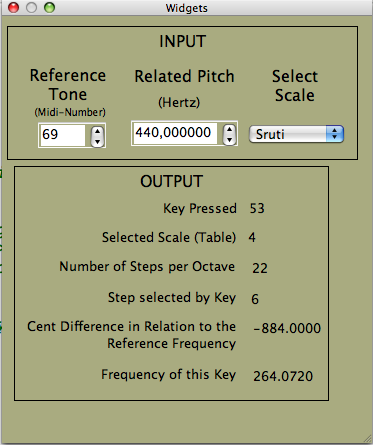
Adding new scales or changing existing ones is done by adding/changing the function tables at the beginning of the CSD, and the menu titles in the QuteCsound Widget Panel. If you would like to select the scales by shortcuts or by some reserved MIDI keys, you can use portions of the code shown above in tune_05a and tune_05b.
As all the examples are related to tuning, this allows you to explore all the possibilities in Csound for employing your own sounds when a MIDI key is pressed. A very simple variation could be replacing the sine tones with a plucked string sound, as shown in tune_07a.
VIII. Conclusion
Csound seems to be often underestimated in respect to its capabilities for live performance. I tried to show how you can code in a simple and straightforward manner Csound instruments which allow you to play in any scale you like on your MIDI keyboard, either for historical studies or for your own compositions or improvisations. You just need to type in a list of cents, then you will have the tuning you want and with any sound you can synthesize in Csound for arbitrary "polyphonic" playing.
Acknowledgements
Thanks to Anna for the corrections, to Steven and Jim for their interest in this subject, and to Andrés for the pleasure of working in QuteCsound. I would like to dedicate this article to the participants of the workshop I gave in Tehran, Iran, this Spring.
References
[1] This is, by the way, NOT the same as the "well-tempered" scale which is used by J. S. Bach, and is the title of his famous collection. In ancient music, a system is "well-tempered", if you can play all major and minor scales in it (without dying of ear pain). So there are MANY "well-tempered" scales (Kirnberger, Werckmeister and others) in this time and also before. NONE of it was "equal-tempered". In an equal-tempered scale, one major scale sounds like any other, and so do the minor scales. The only difference is the absolute pitch. So there are many "well-tempered" tunings in history, but there is just one "equal-tempered".
[2]Schoenberg, Arnold. "Method of Composing with Twelve Tones Which are Related Only with One Another" ("Komposition mit zwölf nur aufeinander bezogenen Tönen"). See his lecture "Composition with Twelve Tones"(1941). Style and Idea. ed. L. Stein. London: Faber and Faber Ltd.,1975. p. 218.
[3] I did this in TclCsound, too. It can be downloaded ("Stimmungen") from www.joachimheintz.de/software.
[4] You just must not check the "Ignore CsOptions" checkbox in the Configurations Dialog. You should do something like this:
[5] In QuteCsound you actually do not need this. You can choose your output device in the configuration dialog, or even browse to the one you would like to choose. See the screenshot above.
[6] If you just want one keyboard to receive Csound, you can choose your device using -M0, -M1 etc (also here QuteCsound allows you to browse your MIDI devices in the configuration dialog).
[7] You can also try lower values for -b and -B (e.g. -b64 -B256 or -b32 -B128 or even -b16 -B64). There is an intricate interaction of the ksmps (in the orchestra header), the -b (software buffer size) and the -B (hardware buffer size) flag. It is well described in the relevant section of the manual ("Optimizing Audio I/O Latency"). Refer also to the explanation by Victor Lazzarini regarding the "full duplex audio" mode when using realtime audio in (-iadc and -odac) in http://www.nabble.com/pvsbufread%2C-ksmps-and-ghosts-over-p3-to23684045.html#a23707140.
[8] The exact value is 1.9549576.... You can calculate this value by starting from one pitch (say 200 Hz) and then comparing the pure fifth (which has by the ratio 3:2 a frequency of 300 Hz) with the equal-tempered fifth (which is calculated as 200 * 2^7/12 = 299.6614... Hz). Then you get the cent difference of both frequencies by the formula 1200 * log 2 (freq1/freq2). In Lisp: (* 1200 (log (/ 300 (* 200 (expt 2 7/12))) 2)).
[9] The absolute cent values are: 0 - 76 - 193 - 310 - 386 - 503 - 579 - 697 - 773 - 890 - 1007 - 1083. See Klaus Lang, "Auf Wohlklangswellen durch der Töne Meer, Temperaturen und Stimmungen zwischen dem 11. und 19. Jahrhundert", Graz 1999, p. 68, now online available under http://iem.at/projekte/publications/bem/bem10/.
[10] The negative number for the Gen-Routine (-2) avoids the normalization of the values we put in the list. The negative number for the size of the function table (-12) allows Csound accept non-power-of-two tables.
[11] Without the widget specifications. They are included in the attached example files.
[12] A better one would probably be to calculate the frequency of a pitch without comparing it to the cpsmidinn values. This is more or less the way we will go in tune_07.csd, where we have more than 12 steps per octave.
[13] The absolute values are: 0 - 114 - 204 - 294 - 408 - 498 - 612 - 702 - 816 - 906 - 996 - 1110. Klaus Lang (see above), p. 41.
[14] Sambamoorthy, P. South Indian Music. Book IV, Second Edition, Madras 1954, pp 95-97.
[15] Probably there could be a more elegant solution, but this seems to do what it should do.